Asymptotic Notations

What is Asymptotic Notation?

Imagine you’re trying to see how fast an algorithm is as your input size grows. You don’t care about small details like:

The brand of your CPU
Whether you used i++ or i += 1
Exact number of milliseconds

Instead, you want to know: 💡 “What happens when my input gets HUGE?”

That’s where asymptotic notation comes in. It’s like short-hand math for describing growth rates of algorithms.

Why do we need it?

Ignore constants and small terms — focus on the big picture.
Compare algorithms fairly — across different machines.
Predict scalability — how well will it handle massive input.

Example:

Algorithm A takes 0.05n² + 2n + 3 operations.
Algorithm B takes 100n + 10 operations.

For small n, B might be slower due to the big constant 100. But as n grows, n² will crush n, so A will eventually be much slower.

The Main Asymptotic Notations

There are five primary notations you’ll see often.

Big O — Upper Bound

Definition: Describes the worst-case growth rate. It tells you: “It won’t grow faster than this.”

Formal idea:

f(n) = O(g(n))  means  f(n) ≤ C × g(n)   for some constant C, for large enough n.

Example: If an algorithm takes 3n + 2 steps, then it’s O(n). It won’t ever grow faster than some multiple of n.

You use Big O for:

Worst-case runtime (common in competitive programming).
Space complexity upper bound.

Big Omega (Ω) — Lower Bound

Definition: Describes the best-case growth rate. It says: “It will take at least this much time.”

Formal idea:

f(n) = Ω(g(n))  means  f(n) ≥ C × g(n)   for some constant C, for large enough n.

Example: If you must check every element at least once, best case is Ω(n).

Big Theta (Θ) — Tight Bound

Definition: Describes an exact growth rate. It says: “It grows at this rate, no faster, no slower (asymptotically).”

Formal idea:

f(n) = Θ(g(n))  means  it’s both O(g(n)) and Ω(g(n)).

Example: 5n + 3 is Θ(n) because:

Upper bound is O(n)
Lower bound is Ω(n)

Think: Θ is like pinning it down exactly.

Little o — Strictly Less Than

Definition: Describes that a function grows strictly slower than another.

Formal idea:

f(n) = o(g(n))  means  f(n) grows slower than g(n), and ratio → 0 as n → ∞.

Example: n is o(n²) because as n grows, n / n² = 1/n → 0.

Little omega — Strictly Greater Than

Definition: Opposite of little o. Function grows strictly faster.

Formal idea:

f(n) = ω(g(n))  means  f(n) grows faster than g(n), and ratio → ∞ as n → ∞.

Example: n² is ω(n) because n² / n = n → ∞.

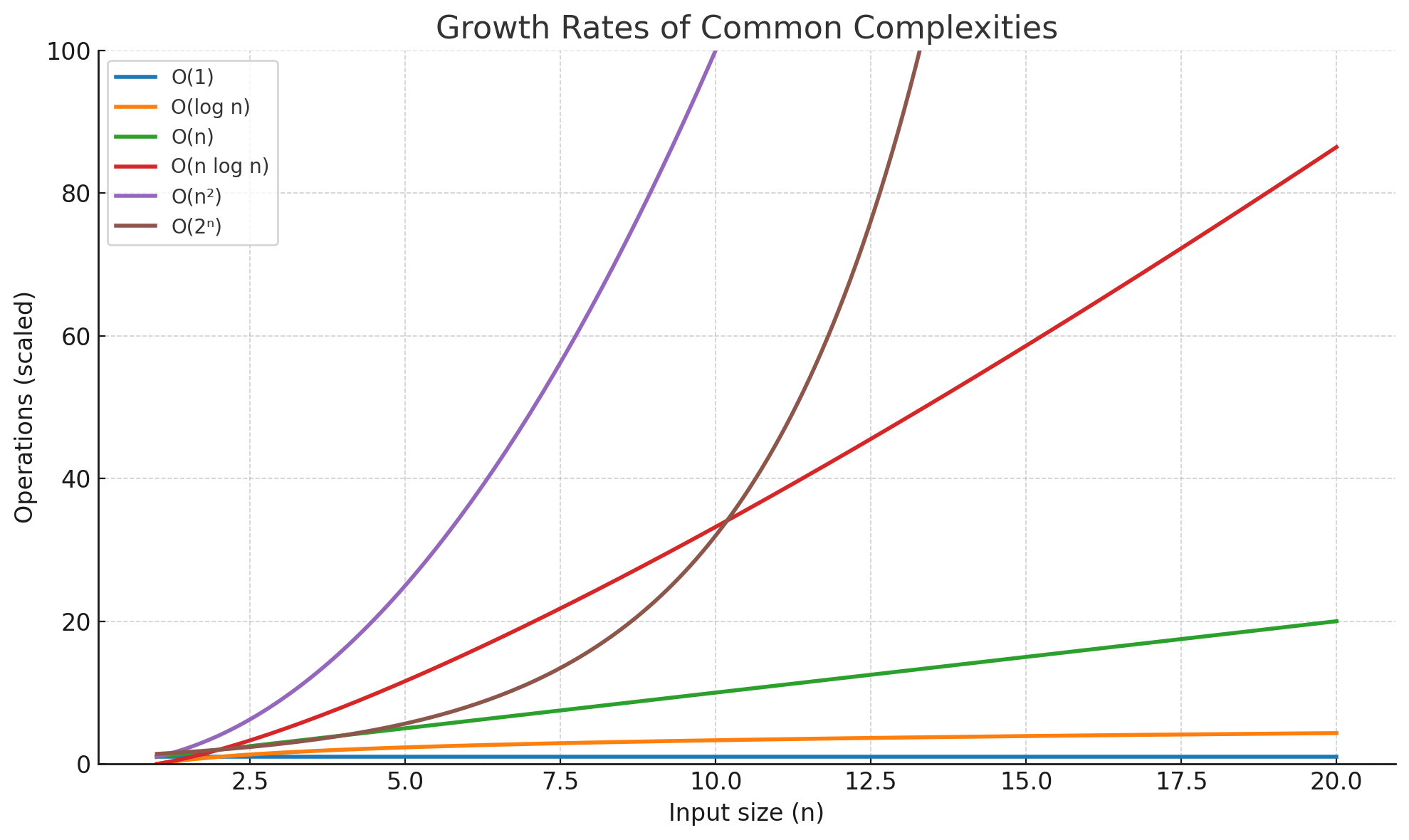
Growth Chart

Order of Growth Cheat Sheet

From slowest to fastest (common ones):

Growth Rate	Name	Example
O(1)	Constant time	Access array element
O(log n)	Logarithmic	Binary search
O(n)	Linear	Loop through array
O(n log n)	Log-linear	Merge sort
O(n²)	Quadratic	Nested loops
O(n³)	Cubic	Triple nested loops
O(2ⁿ)	Exponential	Naive recursive Fibonacci
O(n!)	Factorial	Traveling salesman brute-force

Dropping Constants & Lower-Order Terms

When writing Big O, we only care about the dominant term as n → ∞.

Example: T(n) = 3n² + 10n + 5 → O(n²) Because:

n² dominates for large n
Constants (3, 10, 5) don’t matter.

Best, Worst, and Average Cases

Best case → Often given in Ω notation.
Worst case → Often given in O notation.
Average case → Can also use Θ notation.

Example: Linear search in an array of size n:

Best case (element at start) → Ω(1)
Worst case (element at end or absent) → O(n)
Average case → Θ(n)

Graphical Intuition

If we plotted time vs input size:

O(n) → straight upward slope
O(log n) → rises quickly at first, then flattens
O(n²) → curve gets steep fast
O(2ⁿ) → skyrockets almost immediately

Quick Summary Table

Notation	Meaning	Says What?	Example
O(g(n))	Upper bound	Worst-case	O(n²)
Ω(g(n))	Lower bound	Best-case	Ω(n)
Θ(g(n))	Tight bound	Exact asymptotic behavior	Θ(n)
o(g(n))	Strictly less	Grows slower	o(n²)
ω(g(n))	Strictly more	Grows faster	ω(n)